Calculando distâncias com SQL
Neste artigo vamos aprender como calcular a distância entre duas coordenadas. Para calcular a distância, vamos precisar da latitude e da longitude do local de origem e do local de destino. Vamos ver 3 formas de fazer isso.
Antes de começar, uma pequena aula de geografia
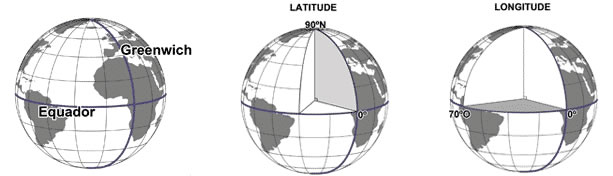
A nossa posição é referenciada em relação a linha do equador e ao meridiano de Greenwich e é expressa em dois valores: a latitude e a longitude. Para saber nossa localização, basta saber a latitude e a longitude.
A latitude é a distância ao Equador medida ao longo do meridiano de Greenwich. Esta distância mede-se em graus, podendo variar entre 0º e 90º para Norte(N) ou para Sul(S).
A longitude é a distância ao meridiano de Greenwich medida ao longo do Equador. Esta distância mede-se em graus, podendo variar entre 0º e 180º para Leste(E) ou para Oeste(W).
Meridiano é qualquer semi círculo máximo que contenha os dois polos de um planeta. Os meridianos dividem a Terra como se ela fosse uma laranja com gomos. Um meridiano que recebe nome especial é o de Greenwich, em referência à cidade de mesmo nome, na Inglaterra. Medem 20 mil quilômetros.
O meridiano de Greenwich é também chamado de meridiano inicial ou de referência, pois é usado como referência para dividir a Terra nos hemisférios Ocidental e Oriental. Cada meridiano corresponde a um antimeridiano, no lado oposto da esfera terrestre.
Chamamos de círculo meridiano o conjunto de dois meridianos opostos. Cada círculo meridiano contém um meridiano e o respectivo meridiano contrário (antimeridiano). Em cada meridiano a longitude é constante. A posição sobre um determinado meridiano é dada pela latitude.
A linha do Equador é uma linha imaginária traçada no ponto exato de igual distância entre o extremo norte da Terra e o extremo sul, sendo, por isso, o principal paralelo terrestre, além de possuir, por definição, a latitude de 0º. Sua principal função é dividir o hemisfério norte e o hemisfério sul.
Depois desta introdução, vamos ao nosso exemplo, vamos calcular a distância entre dois pontos, como referência vou calcular a distância do centro de São Paulo até a praça Panamericana, que é uma praça bem conhecida da zona oeste da cidade. Você pode ver abaixo um mapa do Google Maps entre estes dois pontos.
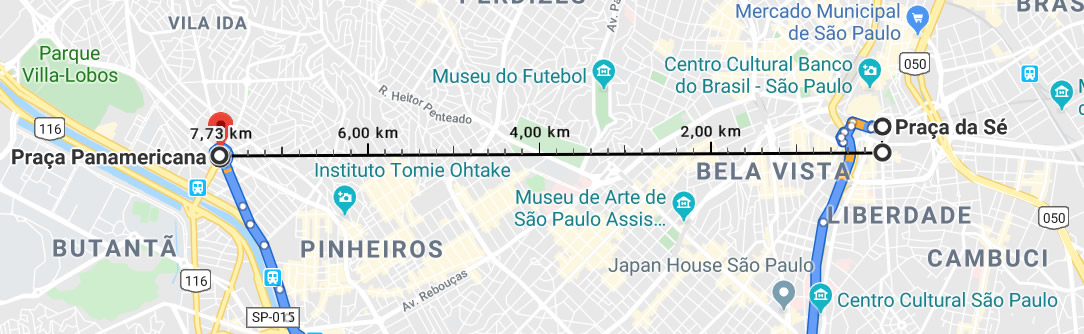
Para fazer o cálculo das distâncias, vamos criar uma tabela e depois cadastrar as coordenadas de origem e de destino.
Observação: Um site que permite pesquisar por endereços e retornar as coordenadas é o https://www.mapcoordinates.net/pt
SQL SERVER
CREATE TABLE [tabela_origem_destino](
[id] [int] IDENTITY(1,1) NOT NULL,
[origem] [varchar](50) NULL,
[latitude_origem] [float] NULL,
[longitude_origem] [float] NULL,
[destino] [varchar](50) NULL,
[latitude_destino] [float] NULL,
[longitude_destino] [float] NULL
) ON [PRIMARY]
MYSQL
CREATE TABLE `tabela_origem_destino` (
`id` int(11) NOT NULL,
`origem` varchar(50) COLLATE latin1_general_ci NOT NULL,
`latitude_origem` float NOT NULL,
`longitude_origem` float NOT NULL,
`destino` varchar(50) COLLATE latin1_general_ci NOT NULL,
`latitude_destino` float NOT NULL,
`longitude_destino` float NOT NULL
) ENGINE=InnoDB DEFAULT CHARSET=latin1 COLLATE=latin1_general_ci;
As coordenadas destes dois pontos são as seguintes:
Praça da Sé
Latiude -23.55039605
Longitude - -46.63308255
Elevação 764m
Praça Panamericana
Latitude = -23.5537232
Longitude - -46.7079569
Elevação 728m
Vamos inserir os dados em nossa tabela de testes
insert into tabela_origem_destino (origem, latitude_origem, longitude_origem, destino, latitude_destino, longitude_destino)
VALUES ('Praça da Sé', -23.55039605, -46.63308255, 'Praça panamericana', -23.5537232, -46.7079569)
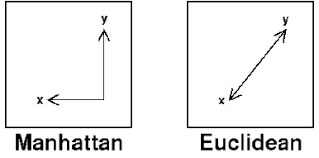
Existem várias formas de calcular a distância entre dois pontos, vamos ver três formas que são comuns, a distância Euclidiana, a distância Manhattan e o Harvesine.
A distância Euclidiana é definida como a soma da raiz quadrada da diferença entre x e y em suas respectivas dimensões.
Já a distância Manhattan tem uma definição mais simples na qual é apenas a soma das diferenças entre x e y em cada dimensão.
Abaixo segue a representação matemática dessas duas medidas:
Distância Euclideana: √((x1 – x2)² + (y1 – y2)²)
Distância Manhattan: |x1 – x2| + |y1 – y2|
Para entender qual a diferença entre ambos, vamos a alguns exemplos. Imagine que você vai calcular a distância entre dois locais e o meio de transporte que vai ser utilizado é um avião. A distância Euclidiana seria o segmento de uma reta na qual indicaria uma possível rota, seria a hipotenusa de um triângulo
Agora, se você for calcular a distância entre dois pontos dentro de uma cidade, o caminho entre estes pontos não vai ser em linha reta, já que existem várias ruas no meio do caminho. Neste caso, a distância Manhattan seria uma forma mais apropriada de calcular, já que ela vai considerar um segmento de retas tanto na vertical quanto na horizontal, geometricamente seria a soma dos catetos. Esta forma de trabalho também é conhecida como "City Block"
Com base em nossa tabela, vamos fazer o cálculo da distância
Euclideana
SQL SERVER
select SQRT(POWER(latitude_origem-latitude_destino,2)+POWER(longitude_origem-longitude_destino,2)) * 111.19 FROM tabela_origem_destino
MYSQL
SELECT SQRT(POW(latitude_origem-latitude_destino, 2) + POW(longitude_origem-longitude_destino, 2)) * 111.19 FROM tabela_origem_destino
Manhattan
SQL Server e MYSQL
select ((latitude_origem-latitude_destino)+(longitude_origem-longitude_destino)) * 111.19 FROM tabela_origem_destino
Perceba que nestes exemplos, foi feita a multiplicação do resultado por 111.19. Esse valor é uma constante que serve para converter o resultado da distância, que é em graus. Você pode substituir este valor por outro, de acordo com a sua necessidade. Um grau de latitude é o equivalente a:
111.19 kilometros
69 milhas
60 milhas náuticas
Considerando o que vimos acima, as respostas são em kilometros. O retorno das distâncias foi 8,33 km utilizando o método Euclideano e 8.69 km usando o método Manhattan. Perceba que o método Manhattan vai calcular um valor maior por causa que ele não vai tentar calcular a distância em linha reta.
Vimos até agora 2 métodos de cálculo de distância. Falta ver mais um, que é o Harvesine.
O nome harvesine é uma abreviação de "HAlf VERsed SINE". Ao contrário dos exemplos anteriores, que fazem o cálculo considerando uma superfície plana, o harvesine considera a distância dos pontos numa superfície esférica.
Segundo a Wikipedia, a fórmula de Haversine é uma importante equação usada em navegação, fornecendo distâncias entre dois pontos de uma esfera a partir de suas latitudes e longitudes. É um caso especial de uma fórmula mais geral de trigonometria esférica, a lei dos Haversines, relacionando os lados a ângulos de uma esfera "triangular".
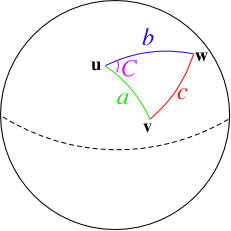
Vamos ver uma implementação deste tipo de fórmula no SQL, a consulta abaixo funciona no SQL Server e no MySQL
select ACOS(SIN(PI()*latitude_origem/180.0)*SIN(PI()*latitude_destino/180.0)+COS(PI()*latitude_origem/180.0)*COS(PI()*latitude_destino/180.0)*COS(PI()*longitude_destino/180.0-PI()*longitude_origem/180.0))*6378.137 from tabela_origem_destino
Perceba que neste exemplo multiplicamos o resultado por uma constante, que foi 6378.137. Este valor é o raio da circunferência da Terra em kilometros. Para obter o resultado em milhas, substitua este valor por 3963.191.
O resultado do cálculo foi 7,64 Kms.
Alguns serviços online, como o Google Maps, podem calcular a melhor rota entre os dois pontos, já que eles consideram as ruas e o tráfego no momento da consulta. Caso você queira comparar o resultado destas operações com o Google Maps, pode consultar este link





